Octavo grado- Los números racionales

En sentido amplio, se llama número racional a todo número que puede representarse como el cociente de dos enteros con denominador distinto de cero. El término racional alude a ración o parte de un todo, y no al pensamiento o actitud racional.

Representación gráfica de las fracciones cuyo divisor es 4.

En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada; de todas ellas, se toma como representante canónico de dicho número racional a la fracción irreducible, la de términos más sencillos.

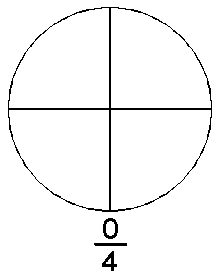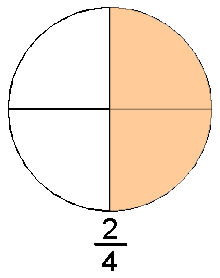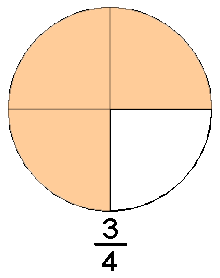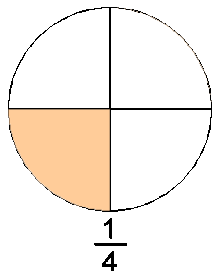
Definimos un número racional como un decimal finito o infinito periódico (por ejemplo, el número decimal finito 0,75 es la representación decimal del número racional 3/4. El número decimal infinito periódico 0,333... es la representación decimal del número racional 1/3).

El conjunto de los números racionales se denota por , que significa "cociente" (Quotient en varios idiomas europeos). Este conjunto de números incluye a los números enteros y es un subconjunto de los números reales. 

La definición de los números Raciones dada en clase, además de las dadas aquí, establece que un número Racional (Q) se obtiene de dividir dos números enteros p/q, donde q es diferente de cero. Quedando el conjunto:

Los números racionales cumplen la propiedad arquimediana o de densidad, esto es, para cualquier pareja de números racionales existe otro número racional situado entre ellos, propiedad que no estaba presente en los números enteros, por lo que los números racionales son densos en la recta de los números reales.

Si colocamos a los racionales en una recta real, podemos encontrar el siguiente caso ejemplo:

Observe que en los puntos en verde se han ubicado algunas fracciones, que corresponden al denominador 2.

Observe detenidamente el siguiente video donde se anima el concepto de los números fraccionarios, recordemos que los números fraccionarios son un subconjunto de los números Racionales.